前回で統計学的検定と相関係数まで終わりました。今回は回帰分析です。
　まず回帰分析には２つの役割があると教えます。「予測」と「交絡変数の調整」（図１）です。今回の講義でこの２つを一通り教えます。 

単回帰分析による予測

　まずは単回帰分析による予測です。使用するのは、今までの講義でも使ってきた身長のデータです。今回用いる身長のデータは「学生の身長」「父親の身長」「母親の身長」「学生の性別」から構成されています。これらを駆使すると重回帰分析を含めて一通りの予測の問題に対応することができます。
　最初に統計モデルという概念を簡単に導入します（図２）。といっても、一次関数のレベルで誤差項のようなものは出しません。独立変数と従属変数という呼び方も教えますが、個人的には説明変数と目的変数のほうが好みなので、こちらを用いることが多いです。

　統計モデルを導入したら、以下（図３）のように回帰分析の結果の見方を先に提示してしまいます。その後に、別のスライドで（この例だと）β₁＝0.31の意味が直線の傾きであること、このβ₁を回帰係数と呼ぶこと、回帰係数の検定は帰無仮説がβ₁＝0であり、β₁が0であるか（その変数に効果があるか）を検定していることを説明します。

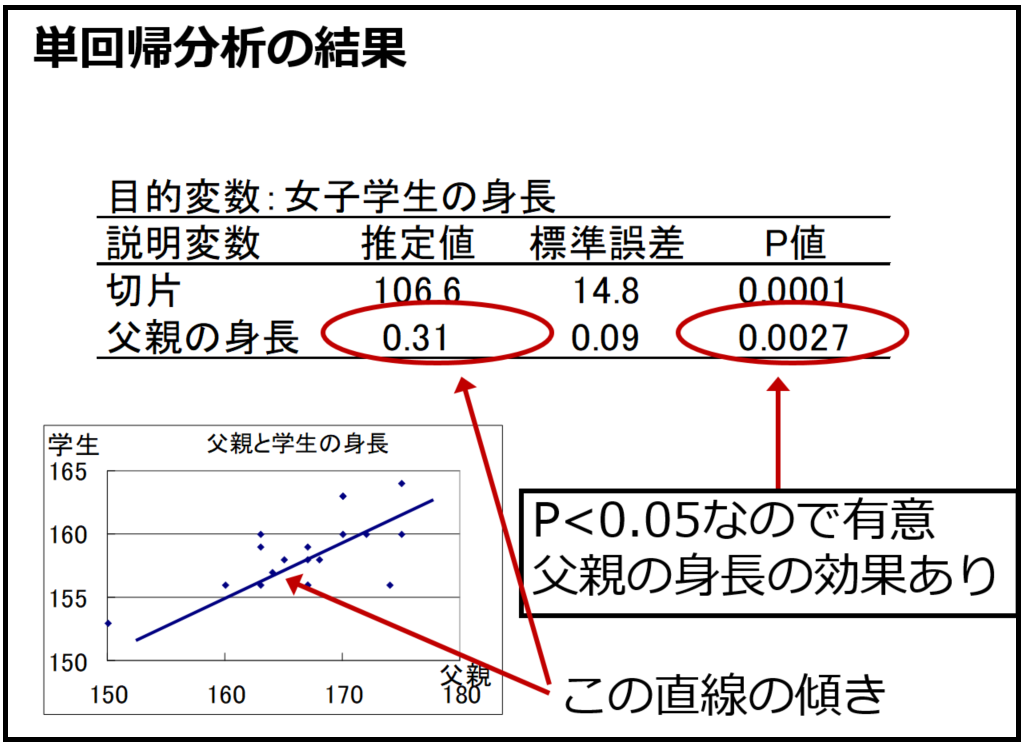
　回帰係数の推定方法については以下（図４）のように、データと予測値の差の2乗和を最小にするように直線を決定するという風に教えますが、具体的な式展開などはしません。

　次が単回帰分析による予測の解釈のまとめのスライド（図５）になります。

平均への回帰

　単回帰分析の後には平均への回帰について教えています。次のスライド（図６）は私が学部生のときに故・大橋靖雄先生から講義を受けたときのものです。

　平均への回帰は難しいですが、知らないと実際に研究をしていて痛い目に合うことがありますので、こういう現象があることは教えています（図７）。この後にゴルトンの身長のデータの例なども出しています。

重回帰分析による予測

　単回帰分析による予測が終わったら、重回帰分析による予測について話します。といっても、重回帰分析は単回帰分析の単なる拡張であるとしか教えていません。スライドはこの１枚（図８）だけです。

モデルのあてはまり

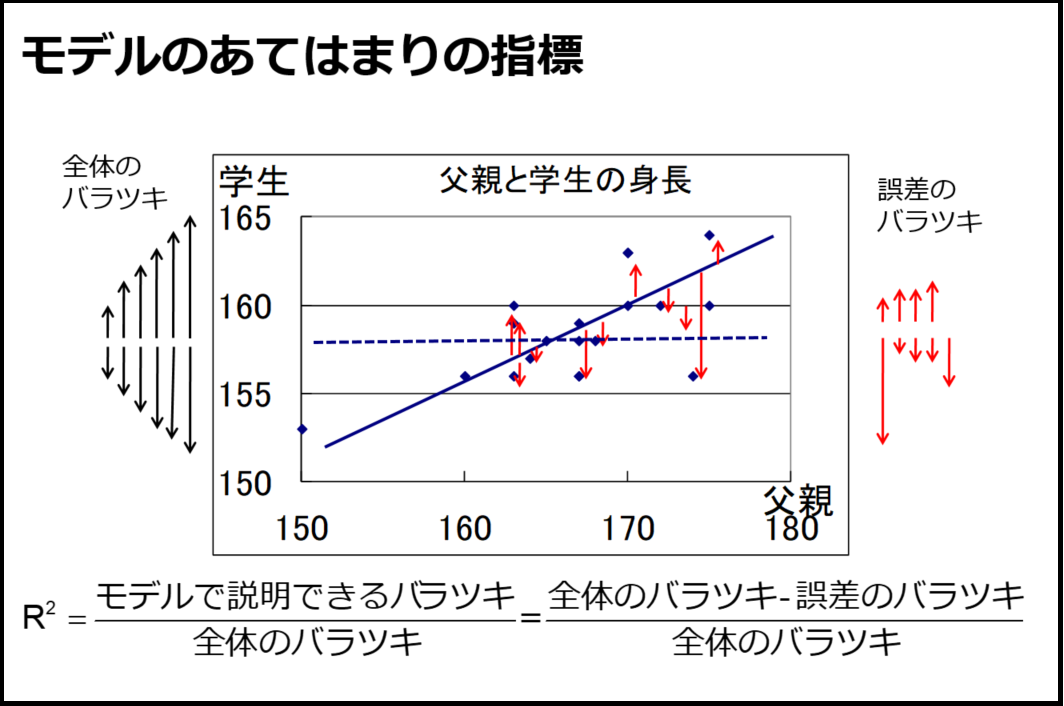
　重回帰分析を１枚のスライドで教えたら、その後は、モデルの当てはまりについて、ここで話しておきます。モデルのあてはまりは決定係数R2や自由度調整済み決定係数Adj-R2の説明を言葉でしつつも、できるだけ視覚的に理解してもらえるよう、以下（図９、10）のように、データのばらつきをどれだけ回帰式が吸収できるか（回帰式を書いても残る誤差はどれくらいか）というスライドを用いています。重回帰分析については３次元のスライドで説明変数が張る平面にデータを射影したスライドを使っていますが詳細な数式の説明などはせず、あくまで直観的な理解だけです。

回帰分析による交絡変数の調整

　最初は交絡の復習です。以前用いた飲酒と肺がん の例を用いて、交絡という現象について復習します。そして、重回帰分析による交絡の調整について話します。使うのは私が執筆した、看護師のがん看護に関する困難感とその関連要因に関する論文です^1）。この例はあまりよい例ではないと思うのですが、日本語の論文であるということ、東北大学病院のデータであるということ、看護師の困難感ということで、身近に感じてもらえる例だと思ってこのデータを使っています。将来的には違うよい論文があればそれにしたいと思っています。
　研究の背景や方法などを説明したのちに、二変量解析の結果と重回帰分析の結果を出して、以下のようなスライド（図11）でまとめています。ちなみに、二変量解析のことを単変量解析ということもありますが、個人的には二変量解析と呼ぶほうが好みです。

ロジスティック回帰分析

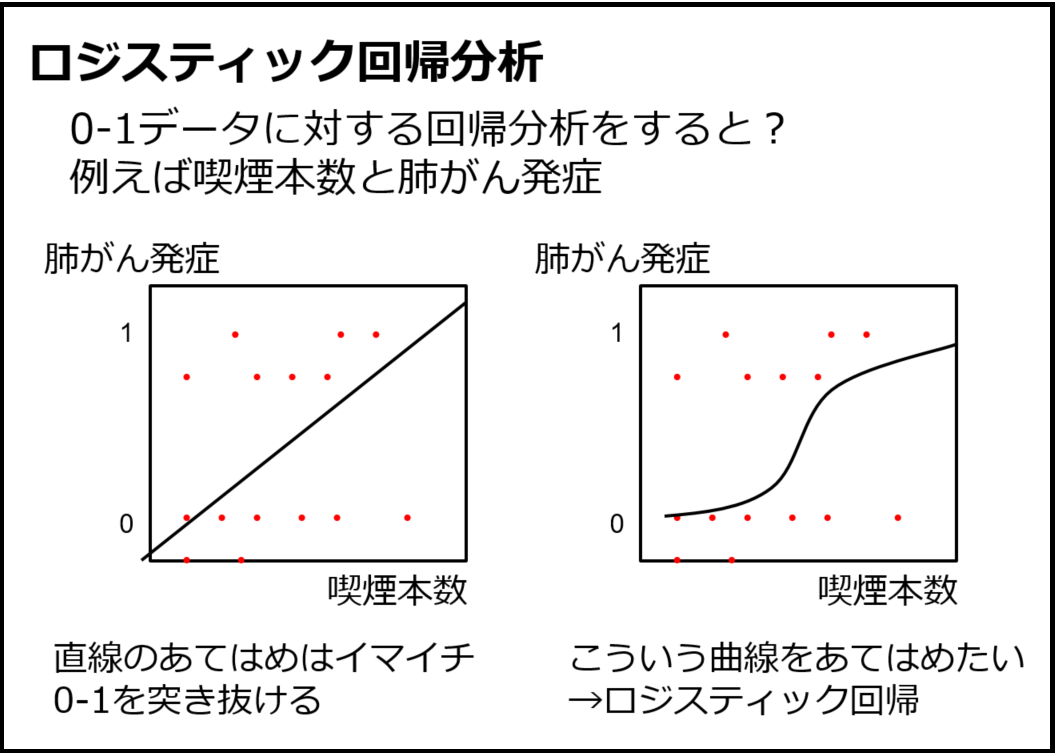
　重回帰分析による交絡調整の話をした後には、２値データに対するロジスティック回帰分析まで説明しています。ロジスティック回帰分析の説明にはどうしても数式を使わざるを得ないのですが、学生にしっかり理解させているわけではなくて、とにかく２値データはロジスティック回帰を使う、オッズ比とは「Xの値が１変化したときに何倍Ｙが起こりやすくなるかを示す」くらいにしか教えていません。このスライド（図12、13、14）と私の説明ではしっかり復習しないと理解できている学生は少ないのでないかと思います。本当はしっかり教えたいのですが、ちゃんとやると30分くらいかかってしまうのではないでしょうか。

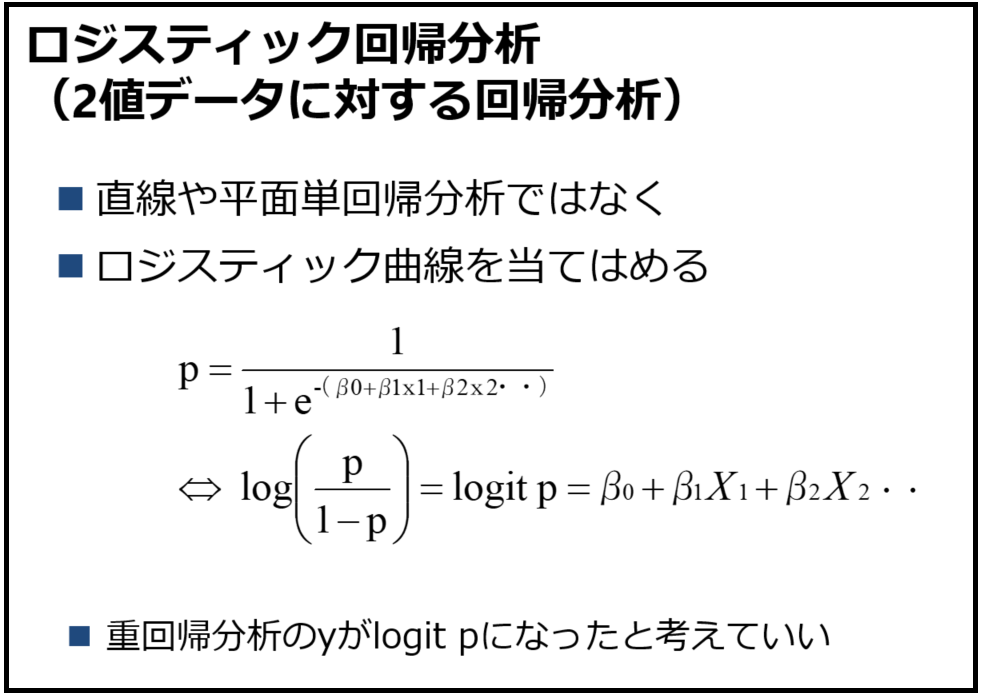
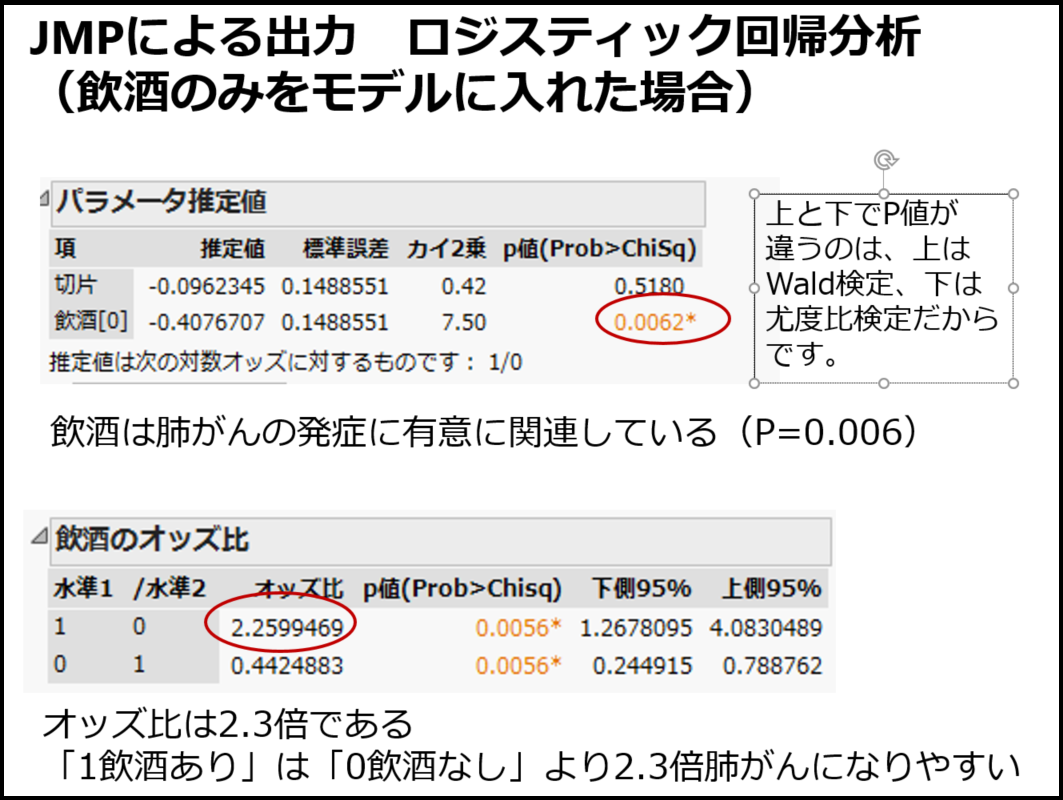
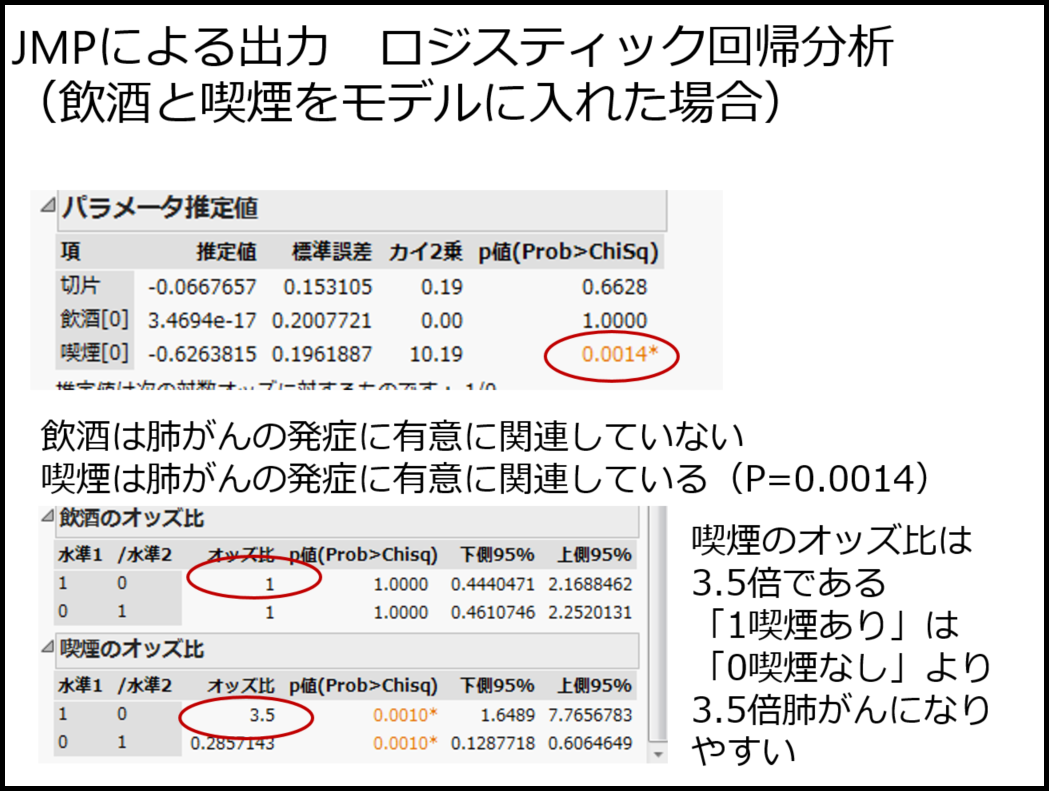
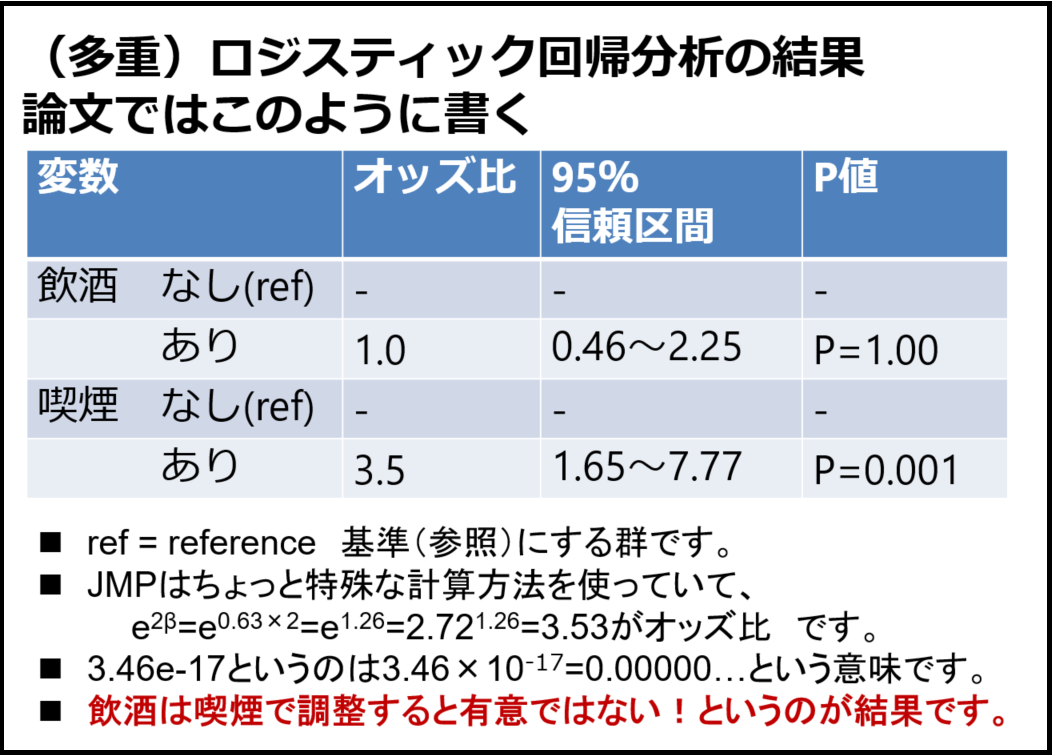
　ロジスティック回帰の理論を説明した後には、飲酒と喫煙の例を用いて解析の実際を説明します（図15、16、17）。本学では統計パッケージJMPが無料で使えるのでJMPの出力を使っています。何度見てもこの結果は美しいですね。 

さまざまな回帰分析

　最後に、今後、論文で出てきたときに「聞いたことがない」とならないようにさまざまな回帰分析について説明しますが、これらは実例を出さずに文字スライドベースです。
　まず二元配置分散分析、共分散分析、数量化一類などは重回帰分析の特殊な形、もしくは全く同じことだと教えています。データの種類によって、ポアソン回帰、比例オッズモデル、対数線形モデル、Cox回帰、反復測定分散分析、一般化推定方程式、混合効果モデルというものが「ある」ということだけ教えます。Cox回帰についてだけ、次回の講義で扱っています。

■その他、多変量解析について知っておきたいこと

　その他知っておきたいこととして、統計学的変数選択・多重共線性・ダミー変数について話します。統計学的変数選択については、まず「よいモデルとは何か」について（図18）話したのちに、変数増加法、変数減少法、ステップワイズ法について話します。個人的には変数減少法が好みです。

 　多重共線性のキースライドは以下（図19）です。重回帰分析の説明に使った看護師の困難感の論文にも多重共線性のチェックのことが出てきますので、それも説明しています。

　ダミー変数は以下のスライド（図20、図21）を使っていますが、どこまで学生が理解しているかよく分かりません。ダミー変数の詳細は試験にも出しませんでした。

　以下が最後のスライド（図22）です。回帰分析による予測の問題と多変量解析による交絡の調整を１回で行うのはかなり厳しいと思っていますが、何回にも分けて詳細に説明したとしても、分からない学生には分からないでしょう。とくに交絡の調整は、実際に論文を読んで慣れるのが一番ではないかと思っています。