はじめに

　前回で要約統計量と確率分布について終わらせ、今回と次回で統計学的仮説検定を扱います。今回は統計学的仮説検定とは何か、統計学的に差があるとはどういうことかということを扱い、次回で実際のさまざまな仮説検定について紹介します。
　2020年から講義で新型コロナウイルス感染症の例をよく使っているのですが、この講義で最初に出すのが以下の記事（図１）です。この「統計学的に有意」ということは何かを理解してもらうのがこの講義の目標です。

　以下のスライド（図２）も以前から使っています。見てわかるように、割合は同じでも例数が変わるとP値が変わるという例で、直観的には例数が増えれば結果の確からしさが変わるのですが、それを数値化する方法としてP値を教えています。

統計学的検定の考え方

　次のスライド（図３）が今回の講義のキースライドです。コイン投げの賭けを例に出してP値を直観的に理解してもらうようにしています。

　これは私と学生がコイン投げの賭けで勝負するという設定で、コインが表だったら学生が私に100円払う、裏だったら私が学生に100円払うというものです。１回目表、２回目表くらいだったら学生は「今日はついていないな」くらいに思うのでしょうが、これが３回、４回と続いたらどう思うか？ そして、その確率はどうだろうと話していきます。
　実際にはP値は「それより極端な値が出る確率」なので、この％をそのままP値にすることは間違っているのですが、これは「正確な表現ではないが、直観的にはこのように理解すると良い」と学生に伝えて≒を用いて話しています。

　まず直観的にP値が小さくなっていくイメージを持ってもらったら、次は帰無仮説を導入します。帰無仮説に基づく検定の思考プロセスは以下の４枚のスライド（図４～７）を用いて教えています。

　この後に「主張したいこと」「それを否定する（帰無仮説）」「それをさらに否定する（対立仮説を採択）」という図を入れているのですが、その図は著作権の関係で今回の記事には載せられず残念です。
　P値についてのまとめのスライドは以下（図８、９）です。ここで、この議論の仕方は高校生のときに習った背理法の考え方に似ていることも話します。

　本来でしたら米国統計学会のP値に関する声明に基づいて話したほうがいいのだと思いますが、数理統計学を全く導入していないので私の講義では難しいなと思っています。その後に、検定統計量や有意水準の話もするのですが、これはおまけ程度のものです。

統計学的検定の実例

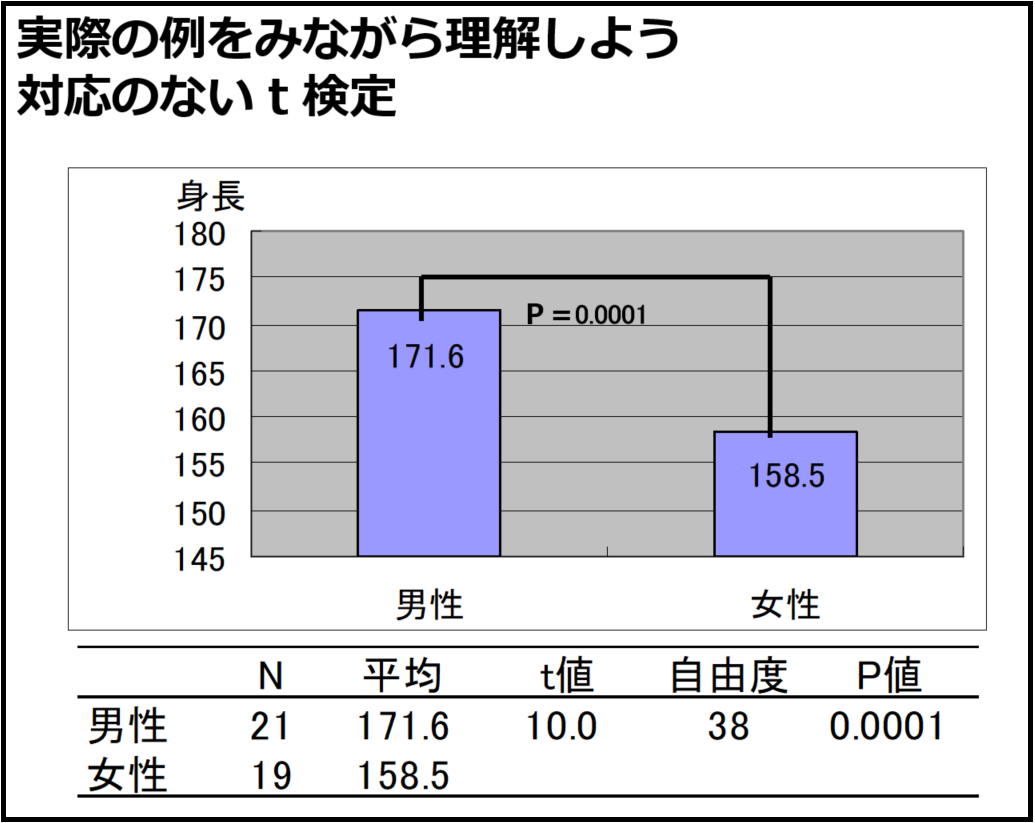
　次は実際のデータで検定を実感してもらいます。最初に検定方法のフローチャートを一瞬見せますが、これは次回やるとして、今回は対応がないｔ検定とカイ２乗検定を説明します。まずは身長のデータを用いた対応のないｔ検定を次のスライド（図10、11）で説明しています。「検定結果の解釈」のスライド（図11）では、カッコに当てはまる内容を学生に答えてもらっています。帰無仮説をしっかり意識してもらうことがポイントだと思っています。

　その次は講義の冒頭部で出した分割表のデータ（図12～15）です。小サンプルの例は、本来はFisherの直接確率検定のほうが適切ですが、ここでは分かりやすさを重視してカイ２乗検定を用いています。Fisherの直接確率検定は次回の講義で扱います。

　ここまで説明してから両側検定と片側検定の話をしますが、私は「両側検定は片側検定を２回しているようなもの」「通常は両側検定を用いる」「私はたぶん１万回以上の検定をしているが、片側検定の経験はほぼ0回です」と教えてしまっています。

αエラーとβエラー

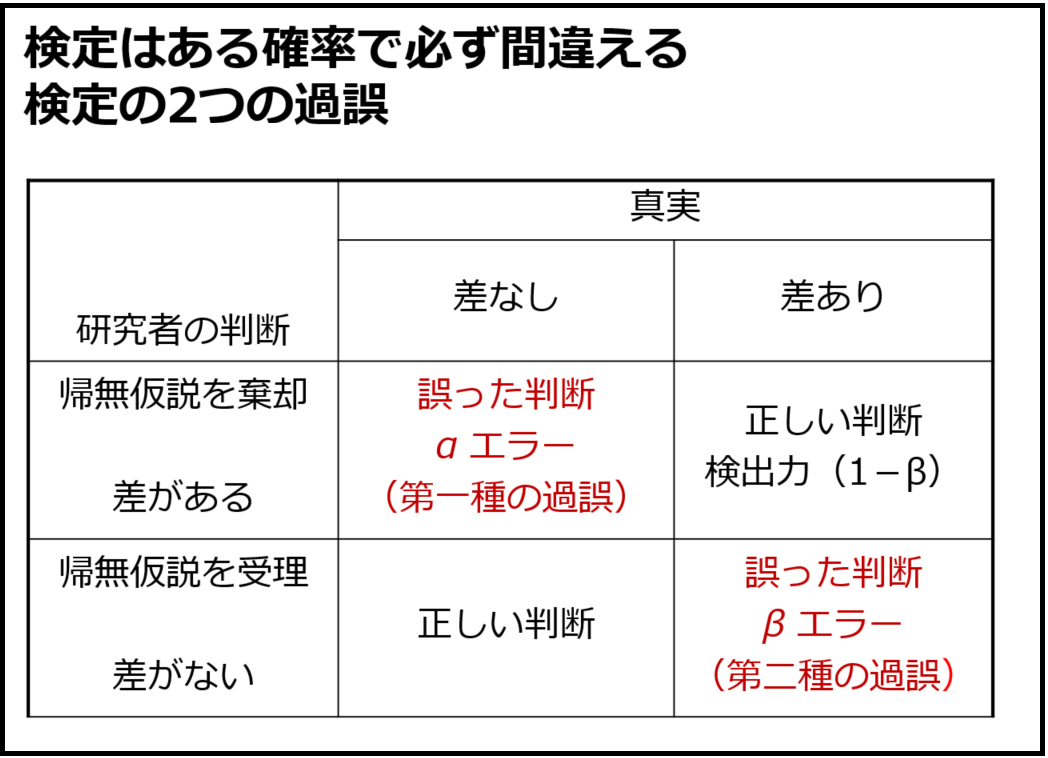
　ここから統計学的検定の各論に入っていきます。まずはαエラーとβエラー、検出力についてです（図16）。過去には帰無仮説に基づく確率分布と対立仮説に基づく確率分布の２つの分布を出して、どの領域がαエラー、βエラー、検出力であるかということを教えていたのですが、これを教えるには「平均の差の分布」という概念を導入せざるを得ず、数理統計学を教えていない学部生には厳しすぎるので現在は言葉だけで教えています。数枚のスライドを用いて言葉で教えても、ある程度は理解できるようです。伝統に基づき、αエラーは「あわてものの間違い」、βエラーは「ぼんやりものの間違い」と教えています。 

検定の多重性

　次は検定の多重性（図17）です。検定の多重性は以下のように余事象のことを教えたあとに、実際にグラフを書いてどれくらいの確率でαエラーが名目水準を超えるかを教えています。具体的には「魔法の水」という例を出して、魔法の水の効果を「風邪」「肥満」「高血圧」「糖尿病」・・・などさまざまな疾患で臨床試験をしたらどれかしらは有意に出るだろう。しかしその魔法の水を薬として承認してしまっていいだろうかという話をします。

　ちなみに、少し前にあるWebサイトで「業界初！有意差、完全保証！！ヒト臨床試験有意差保証プラン」というものを見ました。「通常の臨床試験は有意差が出なかった時点で終了、このプランを用いると臨床試験で有意差が出なかったら、無償で再度ヒト臨床試験を実施します」だそうです。何回臨床試験をやったか報告するか、多重性の調整もするのでしょうかね？
　また、余事象の話が出たので、統計学的検定とは全く関係ないのですがデジタルガチャの話（図18）をちょこっとします。この話は受けがいいです。まあ、この講義の目的はリテラシーなので・・・。

95％信頼区間

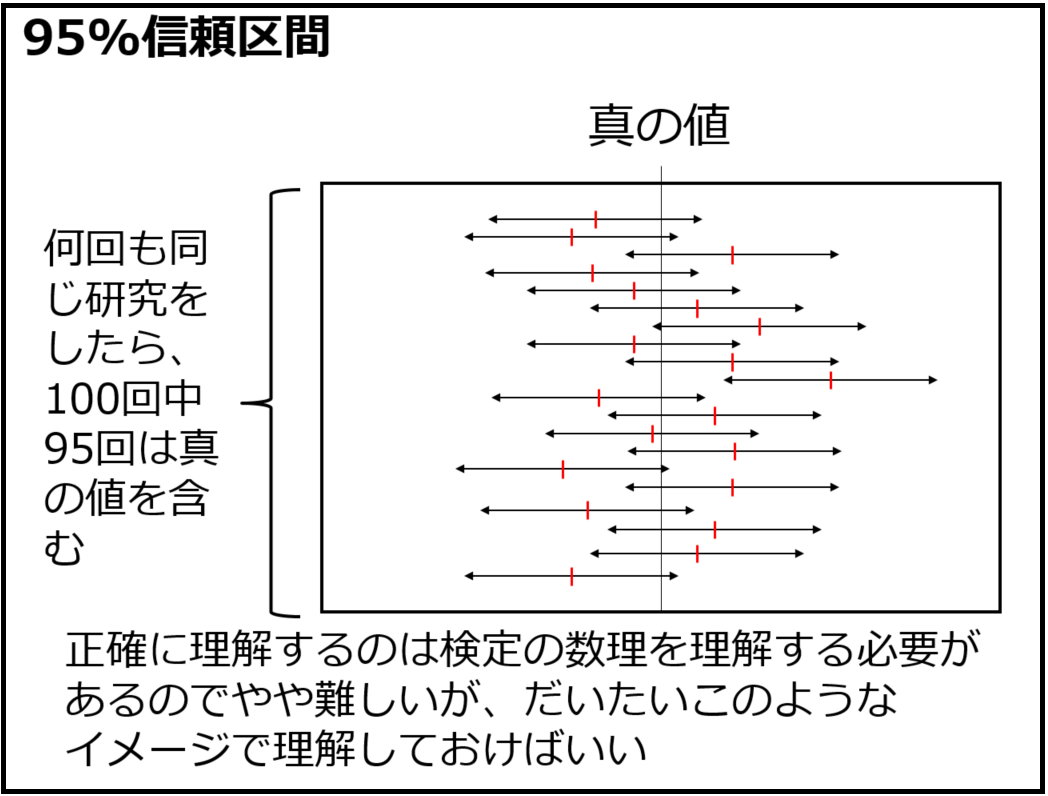
　次は95％信頼区間（図19）です。私は95％信頼区間の説明について、「推定値に幅をつけて確からしさを示すもので、何回も同じ試験と検定を繰り返せば、そのうち95％は真値を含むような範囲」と教えたうえで、正確な表現ではないが「真の値が95％の確率でその範囲にあると考えていい」と教えています。ここも数理統計を学んでいないと厳しいところです。

統計的有意性と臨床的有意性

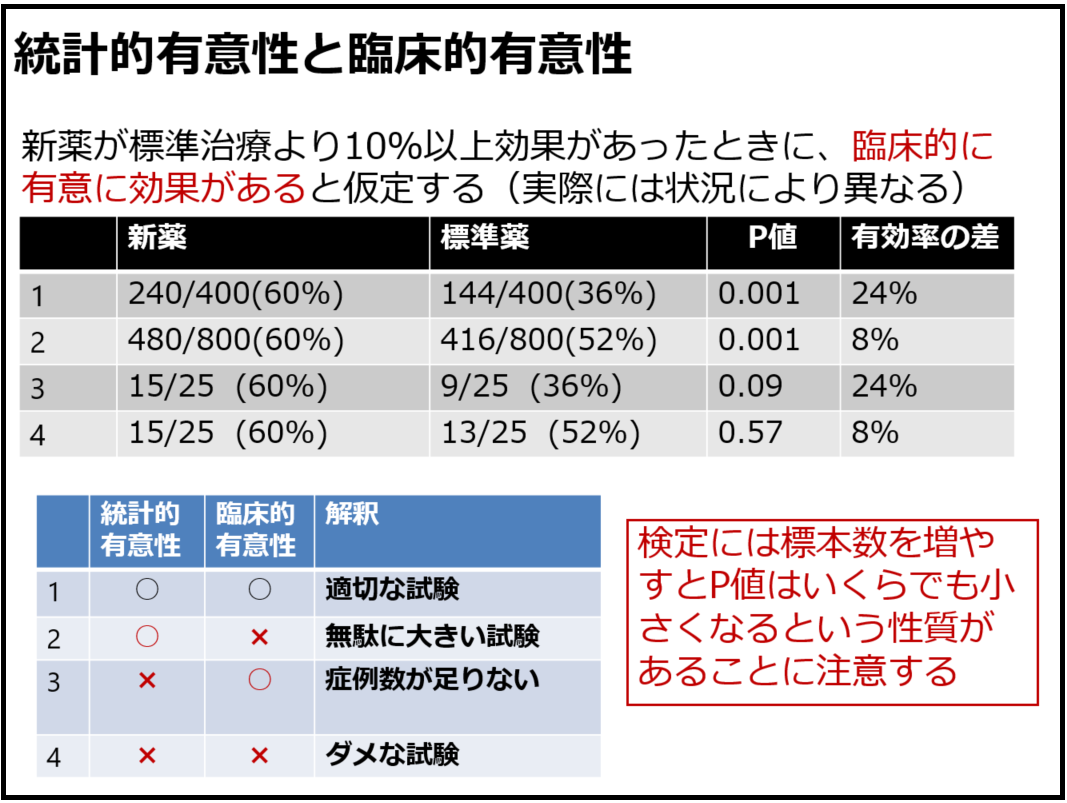
　最後は統計的有意性と臨床的有意性です。これは古典的な数値例を示して、標本数を増やすとP値は小さくなるという性質と合わせて教えています。また、最近の（でもないと思いますが）P値に過度に依存すべきではないという考え方についても教えています。
　今回の記事で紹介するスライドは4枚（図20～23）ですが、実際には効果量などの実例を加えながら10枚くらいのスライドを使って、かなり強調しています。臨床的有意性を考えずに統計学的検定の結果だけで議論している人はいまだに学会などで見かけますね。そのような研究者はセンスがない（統計学が分かっていない）と思われる、学生のみなさんはそうならないようにして欲しいと伝えています。また、統計的有意性・臨床的有意性と研究倫理についても触れています。サンプルサイズ計算は別の回で扱います。

おわりに

　学生には今回の講義は統計の講義の最初のヤマだと最初に話しています。感想はやはり難しかったというものが多いです。次回の講義では、フローチャートを用いて実際の検定方法の選択を行います。